
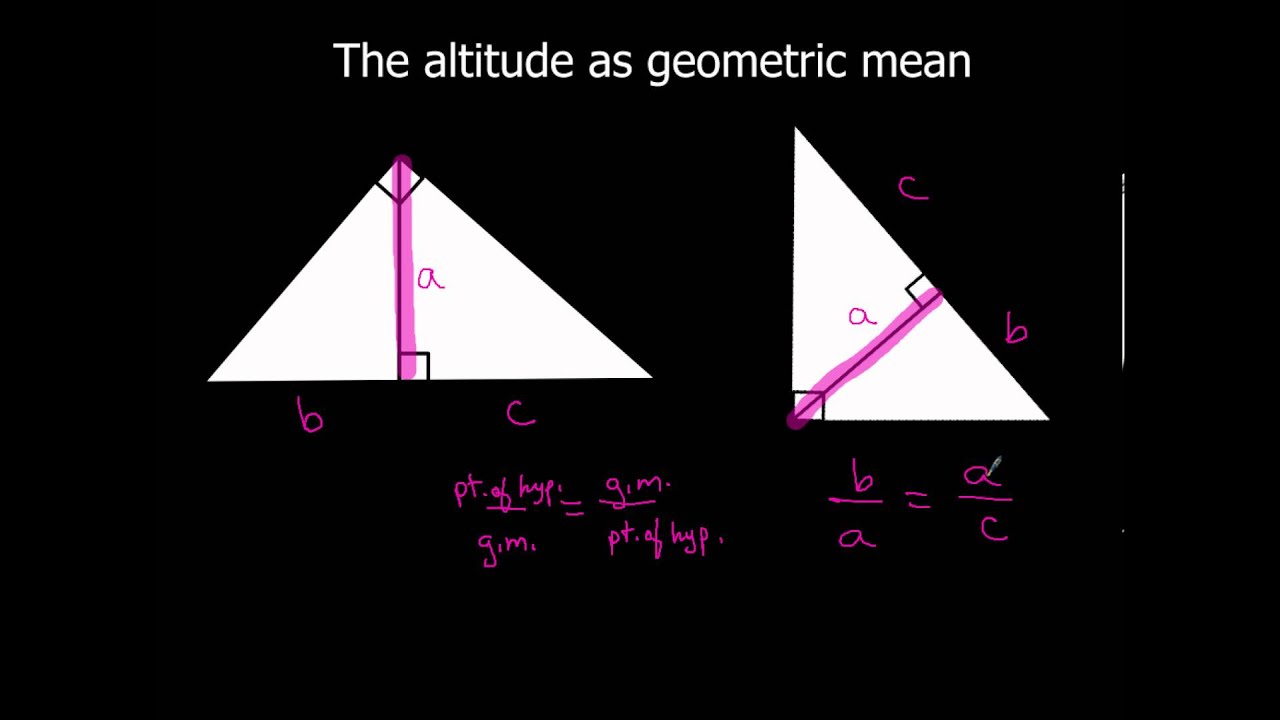
One such arrangement requires a square of area h 2 to complete it, the other a rectangle of area pq. Based on dissection and rearrangement ĭissecting the right triangle along its altitude h yields two similar triangles, which can be augmented and arranged in two alternative ways into a larger right triangle with perpendicular sides of lengths p+h and q+h. Ī division by two finally yields the formula of the geometric mean theorem. | C D | | D E | = | A D | | D B | ⇔ h 2 = p q. Geometric mean theorem as a special case of the chord theorem: Since the altitude is always smaller or equal to the radius, this yields the inequality. Now the altitude represents the geometric mean and the radius the arithmetic mean of the two numbers. For the numbers p and q one constructs a half circle with diameter p+q. Īnother application of provides a geometrical proof of the AM–GM inequality in the case of two numbers. The method also allows for the construction of square roots (see constructible number), since starting with a rectangle that has a width of 1 the constructed square will have a side length that equals the square root of the rectangle's length. Due to Thales' theorem C and the diameter form a right triangle with the line segment DC as its altitude, hence DC is the side of a square with the area of the rectangle. Then we erect a perpendicular line to the diameter in D that intersects the half circle in C.
Now we extend the segment q to its left by p (using arc AE centered on D) and draw a half circle with endpoints A and B with the new segment p+q as its diameter.
For such a rectangle with sides p and q we denote its top left vertex with D. The latter version yields a method to square a rectangle with ruler and compass, that is to construct a square of equal area to a given rectangle.


 0 kommentar(er)
0 kommentar(er)
